
APA Style
Shen Qian, Meng Cheng. (2025). Physical Layer Security in Lossy Untrusted Relay Networks with Finite Blocklength. Communications & Networks Connect, 1 (Article ID: 0004). https://doi.org/10.69709/COConnect.2024.003818MLA Style
Shen Qian, Meng Cheng. "Physical Layer Security in Lossy Untrusted Relay Networks with Finite Blocklength". Communications & Networks Connect, vol. 1, 2025, Article ID: 0004, https://doi.org/10.69709/COConnect.2024.003818.Chicago Style
Shen Qian, Meng Cheng. 2025. "Physical Layer Security in Lossy Untrusted Relay Networks with Finite Blocklength." Communications & Networks Connect 1 (2025): 0004. https://doi.org/10.69709/COConnect.2024.003818.
 ACCESS
Research Article
ACCESS
Research Article
Volume 1, Article ID: 2025.0004

Shen Qian
shen-qian@st.seikei.ac.jp

Meng Cheng
meng.cheng@shnu.edu.cn
1 Department of Science and Technology, Faculty of Science and Technology, Seikei University, Tokyo 180-8633, Japan
2 College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China
* Author to whom correspondence should be addressed
Received: 27 Oct 2024 Accepted: 02 Dec 2024 Available Online: 07 Jan 2025 Published: 18 Mar 2025
In this paper, we examine the physical layer security (PLS) in lossy untrusted relay networks, focusing on finite blocklength transmissions. In such networks, ensuring secure communication is particularly challenging due to the presence of untrusted relay nodes and the inherent limitations of short-packet transmissions. We propose the reliable-and-secure probability (RSP) as a performance metric to evaluate the likelihood that the destination node successfully recovers the transmitted message while untrusted relays experience an outage. Two basic network topologies are taken into consideration, which are the three-node one way network and the single-source multi-untrusted-relay network without direct source-to-destination link. By optimizing power allocation and relay positioning, the RSP can be significantly improved, even when decoding errors occur at the relays. The study demonstrates that lossy decode-and-forward relaying complicates secure communication but also presents opportunities for performance enhancement through careful resource management. Numerical simulations validate the effectiveness of the proposed optimization strategies in enhancing security, especially for applications in ultra-reliable low-latency communication and massive machine-type communication in 5G/6G networks. Future research will focus on deriving more precise closed-form expressions for RSP in finite blocklength settings and investigating machine learning-based approaches for real-time optimization of secure communications in dynamic wireless environments. This study contributes to the growing body of knowledge on PLS in modern wireless systems, offering insights for future advancements.
The increasing reliance on wireless networks for secure communication has introduced new vulnerabilities where traditional cryptographic measures may be insufficient. Physical layer security (PLS) has emerged as a promising alternative, offering a way to secure communications by exploiting the inherent properties of wireless channels, for example, noise, fading, and interference [1,2]. This is particularly critical in networks with untrusted relay nodes, where data confidentiality is at risk due to the presence of intermediary nodes that may not be fully reliable, as shown in Figure 1. Untrusted relay networks introduce a unique set of challenges. These networks often involve relay nodes that assist in forwarding messages, but may attempt to intercept or modify the transmitted data [3,4]. The use of lossy channels further complicates the secure transmission of data, as these channels are prone to signal degradation and higher bit error rates (BER). Such environments require innovative solutions to ensure both the reliability and security of communication, even when relays are untrusted and channels are imperfect [5,6]. Short-packet communication is regarded a key technology for supporting emerging 5G and beyond application scenarios [7]. For instance, in intelligent sensing, short packets are commonly used by IoT devices and sensors in ultra-reliable low-latency communications (uRLLC) and massive machine-type communications (mMTC) [8]. The traditional consideration of wireless transmission with Shannon’s information theory is inadequate for designing infinite-block-length communications or evaluating their performance. With short-packet transmissions, the header length of the package cannot be ignored compared to the payload [9], and (2) limited block-length introduces unavoidable decoding errors and potential information leakage due to backoff from capacity [10]. As a result, short-packet transmissions experience reduced channel capacity, making it more difficult to achieve reliable communication. This paper focuses on the evaluation of PLS in lossy untrusted relay networks, particularly under finite blocklength regimes. In these scenarios, where direct source-to-destination communication is infeasible, relay nodes are essential. However, the trustworthiness of the relays and the lossy nature of the channels present significant security risks. We explore how PLS techniques can be applied to improve the security of these networks, ensuring that confidential messages remain protected even in the presence of untrusted relays. In addition, we examine the role of finite blocklength communication in these systems. Short packet transmissions, a key requirement for uRLLC, introduce challenges in achieving high secrecy rates due to the limited number of channel uses. We investigate the trade-offs between security and efficiency in such networks and propose strategies to optimize performance under these constraints [11]. The following of this paper is organized as follows: Section 2 discusses the fundamental concepts of physical layer security in the context of lossy channels and untrusted relay networks. Section 3 delves into PLS in three-node untrusted lossy one-way relaying. Section 4 focuses on the performance analysis in diamond short-packet communication systems. Section 5 lists some challenges and future research directions for PLS in relay networks. Section 6 concludes the paper.
2.1. Security Threats in Untrusted Relays In wireless communication systems, untrusted relay nodes present several security challenges that can compromise the confidentiality of the data being transmitted. The presence of these relay nodes, which might act as potential eavesdroppers, complicating secure transmission. These challenges arise from the following key factors: Risk of Eavesdropping: Untrusted relays, although intended to assist in signal forwarding, can intercept and decode confidential information. As described in various studies, including, untrusted relays can act as eavesdroppers while forwarding information between two parties. The relay may opportunistically exploit its position to decode and intercept sensitive information without the authorization of the legitimate users [12,13]. Relaying Vulnerabilities: In the relay node amplifies the received signal, amplify-and-forward (AF), which includes both the legitimate data and any noise, or decode the received signal DF and forwards it to the destination. However, if the relay is untrusted, it can potentially decode the signal before forwarding it. This issue is compounded in multi-input multi-output (MIMO) systems, where the untrusted relay could have access to multiple data streams, increasing the chances of successful interception [14,15]. PLS Limitations: while PLS is employed to protect transmissions by exploiting the characteristics of the wireless channel, its effectiveness is reduced when the relay itself is untrusted. The relay may still capture the signal, especially if it is equipped with multiple antennas or operates in full-duplex mode, allowing for simultaneous transmission and reception. This setup enhances its eavesdropping capabilities [16,17].
Mitigating these challenges requires advanced techniques, such as adaptive precoding and cooperative jamming, where the legitimate parties deliberately introduce interference to confuse the untrusted relay, thereby preventing it from extracting useful information.
2.2. Challenges and Opportunities of Lossy Channels on Secure Communication
Lossy channels present significant challenges for information transmission, particularly when implementing PLS. The inherent degradation in signal quality due to noise, fading, and interference increases the bit error rate (BER) and complicates the secure transmission of confidential data. One primary issue is that lower signal-to-noise ratios (SNR) result in higher BER, which makes it easier for legitimate receivers or relays to misinterpret the transmitted message. This potentially leads to compromising the integrity of sensitive information. Traditional PLS approaches, such as artificial noise and cooperative jamming injection, often face challenges in these conditions due to their reliance on the stability and quality of the channel. As the channel fluctuates, these methods become less reliable [18].
In systems that use decode-and-forward (DF) relays, lossy channels can introduce errors in the relayed signals, which untrusted relays could exploit to intercept and decode part of the confidential message [19]. AF relays, on the other hand, amplify both the signal and the noise, complicating the implementation of security measures such as cooperative jamming. Moreover, the randomness and unpredictability of fading conditions could sometimes allow the eavesdropper’s channel to outperform that of the legitimate receiver, eventually reducing the secrecy capacity and compromising the system’s security.
Despite these challenges, lossy channels can also be leveraged to enhance PLS. The natural noise and interference in these channels make it harder for eavesdroppers to reconstruct the original message accurately. Typically, the eavesdropper has imperfect channel knowledge, and as a result, receives a more distorted version of the signal compared to the legitimate receiver. This gives the legitimate user, supported by error correction mechanisms, a greater chance of successfully recovering the message while the eavesdropper struggles to do so [20].
Moreover, lossy channels create opportunities to implement controlled interference techniques such as cooperative jamming and artificial noise injection. By introducing targeted noise that selectively degrades the signal quality at the eavesdropper’s receiver without significantly affecting the legitimate receiver, these methods can obscure the eavesdropper’s ability to decode the transmission. In DF relay systems, lossy channels can be used to introduce controlled errors, making it more difficult for eavesdroppers to extract useful information. While this may introduce additional challenges for legitimate receivers, effective error correction techniques can still allow them to recover the message accurately.
3.1. Physical Layer Security in Untrusted Lossy One-Way Relay Networks In this work, the main focus is on a short-packet transmission system involving three nodes, as illustrated in Figure 2. In this system, a legitimate sender, the source (Alice), communicates confidential data to another legitimate recipient, the destination (Bob), with assistance from an intermediary node (Eve). However, Eve is considered an untrusted relay with low trust level. We consider a single antenna setup due to limitations in power and size. We consider a Time Division Multiple access (TDMA) scheme, where transmission is divided into two distinct time phases. In the 1st time phase, Alice broadcasts the independent and identically distributed (i.i.d.) message
. During the 2nd time phase, the relay node, Eve, attempts to decode After receiving signals from both, Alice and Eve, Bob performs joint decoding to recover the original sequence
. An iterative decoding process with two decoders is used to retrieve Alice’s original messages. The two decoders exchange the decoded bits’ log-likelihood ratios through an interleaver and de-interleaver. 3.2. Channel Type The received signals in Bob and Eva are presented by
is the transmit power, We assume
and that Each of the communication links is assumed to undergo Rayleigh fading. The PDF for the instantaneous SNR
following Rayleigh distribution is expressed as 3.3. RSP (Reliable-and-secure probability) Reliable-and-Secure Probability (RSP) Definition The RSP refers to the likelihood that Bob decodes the information sent by Alice successfully, while the untrusted relay Eva experiences an outage. This probability can be formulated as Here,
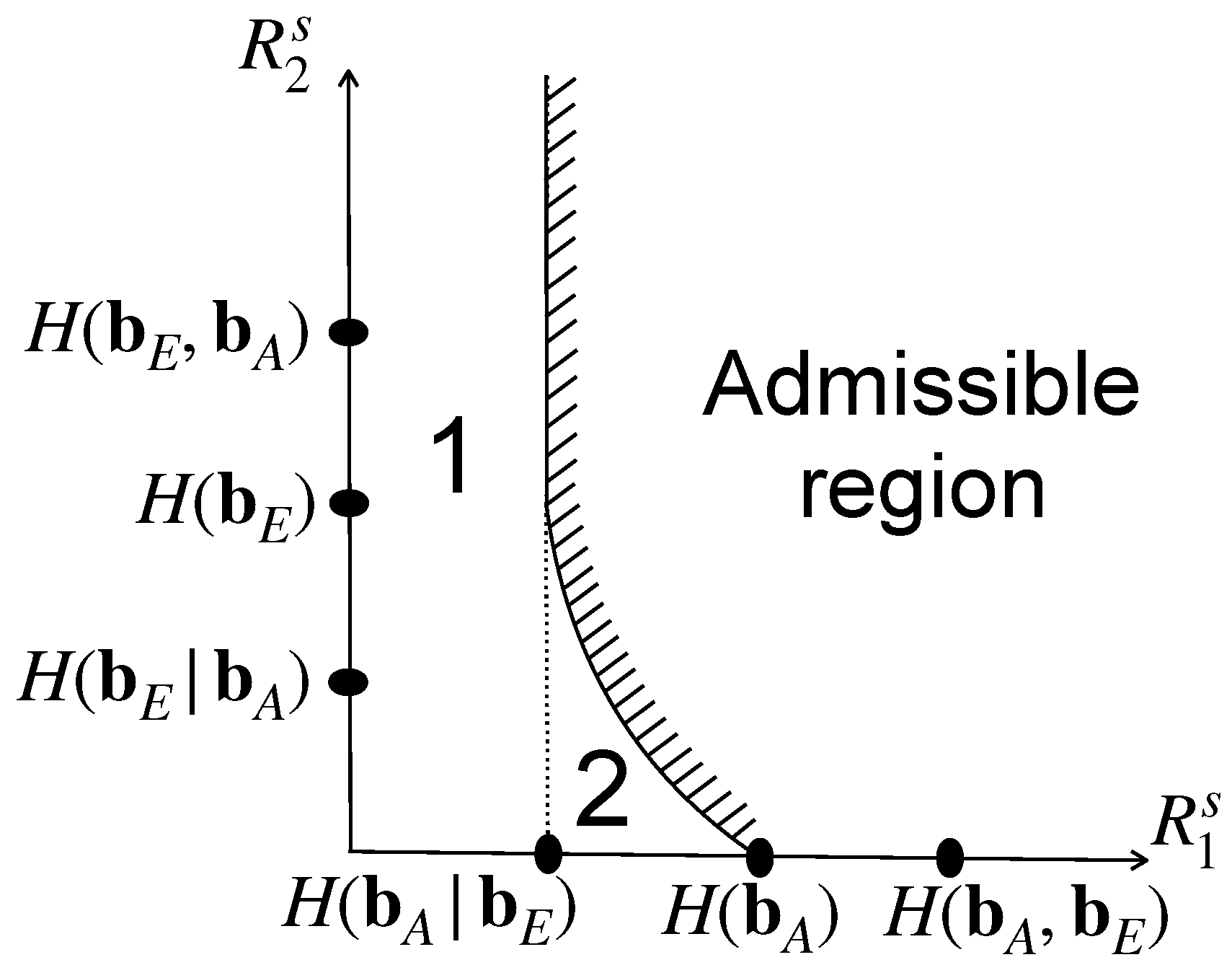
denotes the probability that outage happens at the untrusted relay, while To provide a clearer understanding of the proposed RSP metric, a comparative analysis has been included in the Table 1 with other commonly used metrics in physical layer security. This comparison highlights the unique advantages of RSP in addressing finite blocklength constraints, which are critical for short-packet communications in 5G/6G networks. Comparative analysis of RSP with the other metrics. 3.4. Bob and Eva’s Admissible Rate Region As destination, Bob’s objective is to decode
, the signal In this context,
represents the conditional entropy, while In this paper, we focus on a source that is independently and i.i.d., and thus Equation (6) can be reformulated as
is the binary convolution. With binary source, In accordance with source-channel separation theorem, if The error probability can be reduced to an arbitrarily small value.
and 3.5. Bob’s Outage Probability Since we assume block fading, for a given
, and As defined in Equation (24), the probability
can be expressed as where and These probabilities represent the likelihood that (
, Note that Equations (10) and (11) do not include the case when
, which indicates the perfect decoding at Eva (no outage). When The error probabilities
, and
is the inverse function of With Gaussian source, and The derivation of explicit expressions for Equations (12)–(15) can become highly complicated due to the intricacy of
and 3.6. Optimal Power Allocation Under the total power constraint
, the optimal power allocation corresponds to the point where the maximum RSP is achieved. By normalizing the noise variance for each channel to unity, the average SNR, which corresponds to the transmit power, allocated to Alice and Eva is represented by The main difficulty is determining the optimal k that maximizes the system’s RSP. This involves improving Bob’s capability to correctly decode Alice’s message while simultaneously reducing Eva’s likelihood of intercepting and decoding the original information. The goal is to strike a balance between these two factors, therefore, optimizing the system’s security. This challenge can be formally represented through maximizing the RSP, and the optimization can be formulated as: In theory, by calculating the second-order partial derivative of
with respect to k, the extreme point can be identified, and the convexity can be verified by determining whether the integral results are positive or negative within the range 3.7. Key Insights for RSP Analysis The derived expressions for RSP reveal a fundamental trade-off between ensuring reliable communication at the destination and preventing information leakage at untrusted relays. This highlights the importance of balancing these factors through power allocation. The finite blocklength constraint introduces decoding errors at the relays, which can inadvertently improve security by increasing the likelihood of an outage at the untrusted relay nodes. However, it also necessitates the precise power optimization to maintain reliability. The RSP’s dependence on multiple variables, such as blocklength, SNR, and decoding error probabilities, underscores the need for computationally efficient optimization techniques, especially in dynamic networks. These insights offer valuable guidelines for designing secure wireless systems where short-packet communication is essential, such as in uRLLC and mMTC scenarios.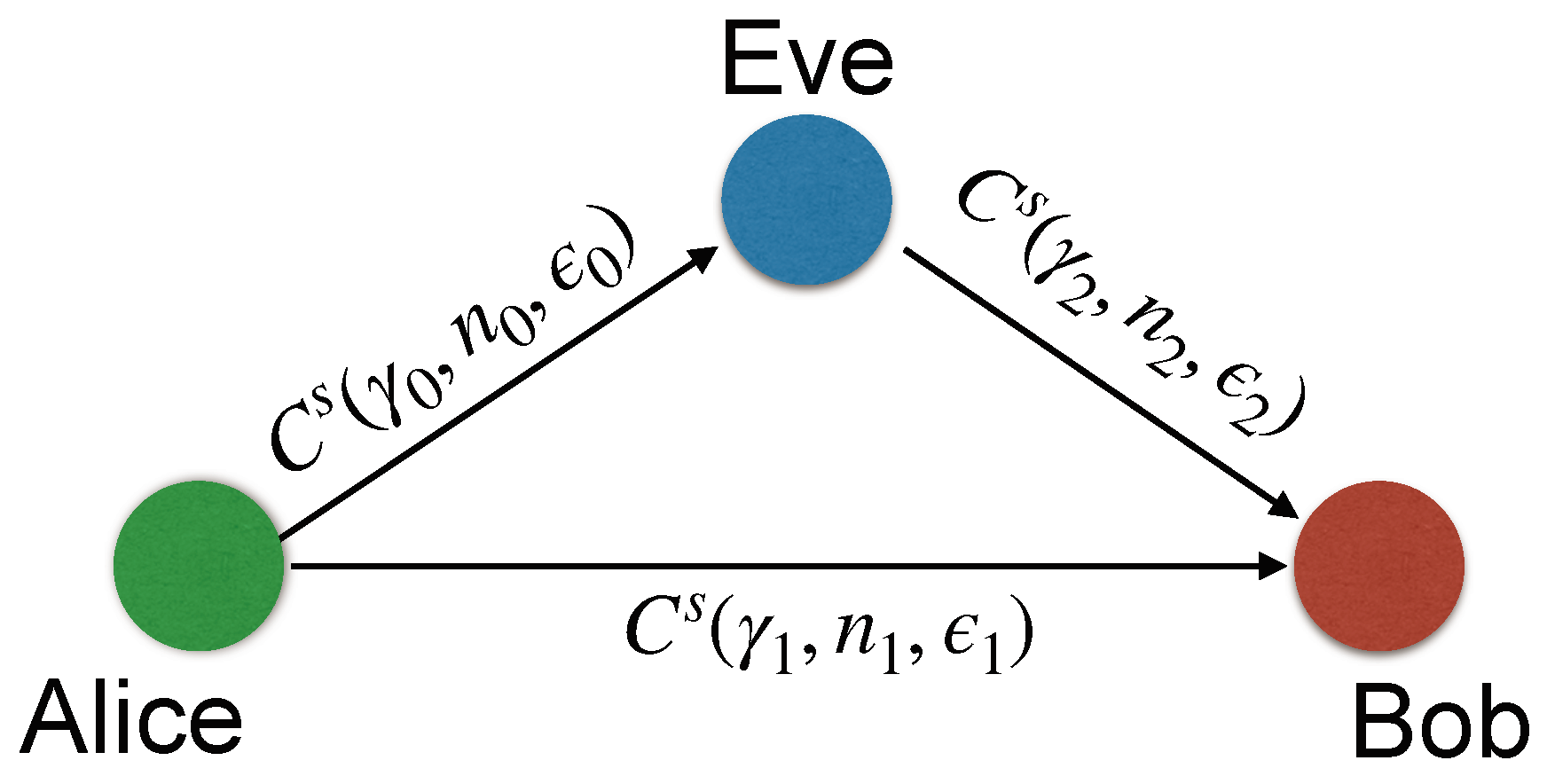
Metric
Definition
Feature
Reliable-and-secure Probability (RSP)
Probability that the legitimate receiver successfully decodes a message while untrusted relays experience an outage
Captures decoding errors and packet length constraints; highly applicable to finite blocklength scenarios
Secrecy Outage Probability
Probability that the eavesdropper’s channel capacity exceeds the legitimate user’s channel capacity
Focuses on channel secrecy without considering finite blocklength constraints
Secure Connectivity Probability
Probability that a secure link is established between source and destination
Measures network-level security but lacks granularity in packet-level reliability
Secure Capacity
Maximum achievable data rate ensuring security against eavesdroppers
Based on Shannon’s infinite blocklength assumptions; not suitable for short-packet transmissions
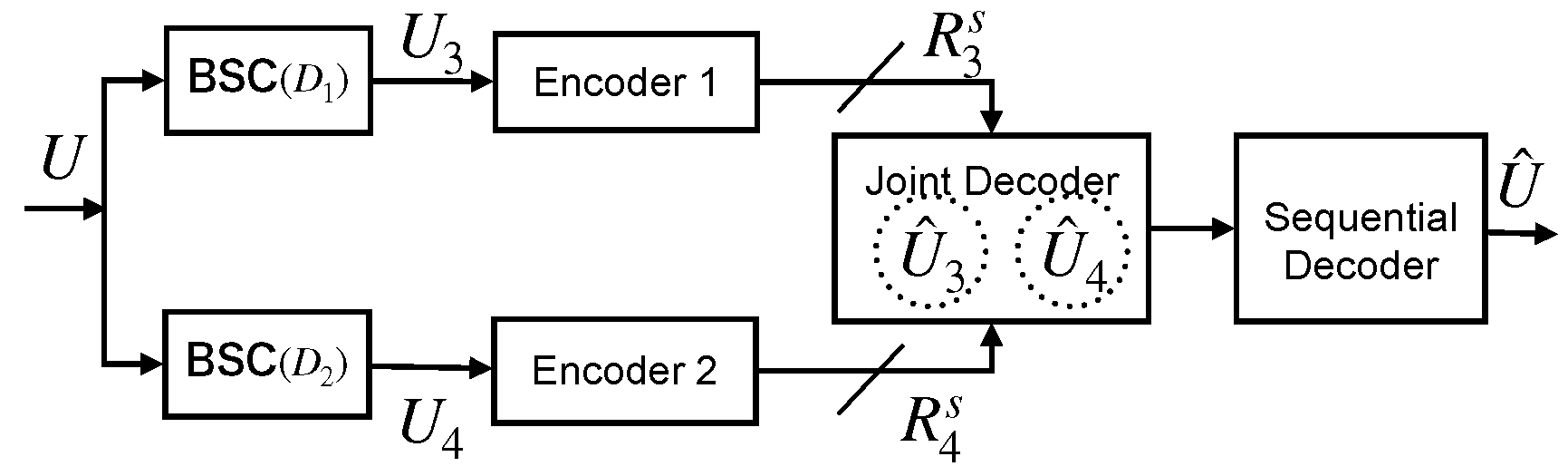
In this section, the focus is on a relay network depicted in Figure 4. A legitimate source, Alice, sends information to another legitimate destination, Bob, with the assistance of two untrusted relays,
( The two intermediate nodes,
and We consider the Alice-to-Bob transmission is split into two time slots. In the 1st time slot, Alice encodes, modulates, and broadcasts the confidential i.i.d. binary information sequences. These sequences follow a Bernoulli
In the system, Lossy DF is employed at
and Once Bob receives the signals from
and 4.1. Short Package Transmission Channel capacity is often regarded as a fundamental performance metric in traditional wireless communication systems. Typically, performance analyses assume an infinite block-length, which leads to the derived performance limits serving as upper bounds. However, in practical scenarios such as uRLLC and mMTC, the infinite packet-length assumption is no longer appropriate to evaluate the performance of secrecy. Additionally, short-block communications offer a solution for reducing delays, making them ideal for applications which is time-sensitive, by minimizing transmission latency [25]. The maximum rate for finite packet-length (short-block) communications, corresponding to
(channel capacity with short-block), is provided by [26]
is the conventional Shannon’s Gaussian channel capacity. n, e and
are Euler’s number and inverse Q-function 4.2. Channel Model Let
where n represent the symbols’ timing index, under an orthogonal transmission assumption. We omit the symbol indices in the subsequent sections for brevity.
denotes the coded transmit symbol.
refers to the gain of the corresponding channels.
represent received signal.
indicate AWGN. Let
and 4.3. Definition for Reliable-and-Secure Probability The objective is to transmit messages to Bob, while ensuring that untrusted relays cannot access the confidential information. A common way is to transmit the information sequences at a rate lower than the secrecy rate [28] from Alice to Bob. However, if there is no direct link between Alice and Bob, it is not possible to achieve the secrecy rate [13]. With lossy DF employed at the relays, decoding errors are permissible at Eva. The decoded message at the Eva are then re-transmit to Bob after re-encoding. Same as the previous section, we define the RSP with the probability that Bob successfully decodes the message sent by Alice, while an outage occurs at
and Here,
represents the outage probability at both untrusted relays. Meanwhile, 4.4. Analyses for Relay-Destination Links’ Error Probability Due to the lossy DF setup, errors are permitted in the untrusted relay-destination links (Alice-
and Alice- based on the theorem of source-channel separation coding with distortion ([21], Theorem 3.7), with distortions
and With binary source following Bernoulli(p) distribution, Here,
represents the entropy function. For Gaussian source, with distribution
. It should be noted that the minimum distortions
and Based on Equations (18) and (25), the contact between
and for Bernoulli(
) sources. Whereas for Gaussian sources 4.5. Outage Probabilities at
Eva
1
and
Eva
2
In short-packet communications,
in Equation (24) is defined as the scenario where the transmission rates
represents During each fading phase, quasi-static fading channel behaves equivalently to an AWGN channel. The gain of channel remains constant within each phase but varies from phase to phase, based on channel fading distributions. As a result, the outage probability
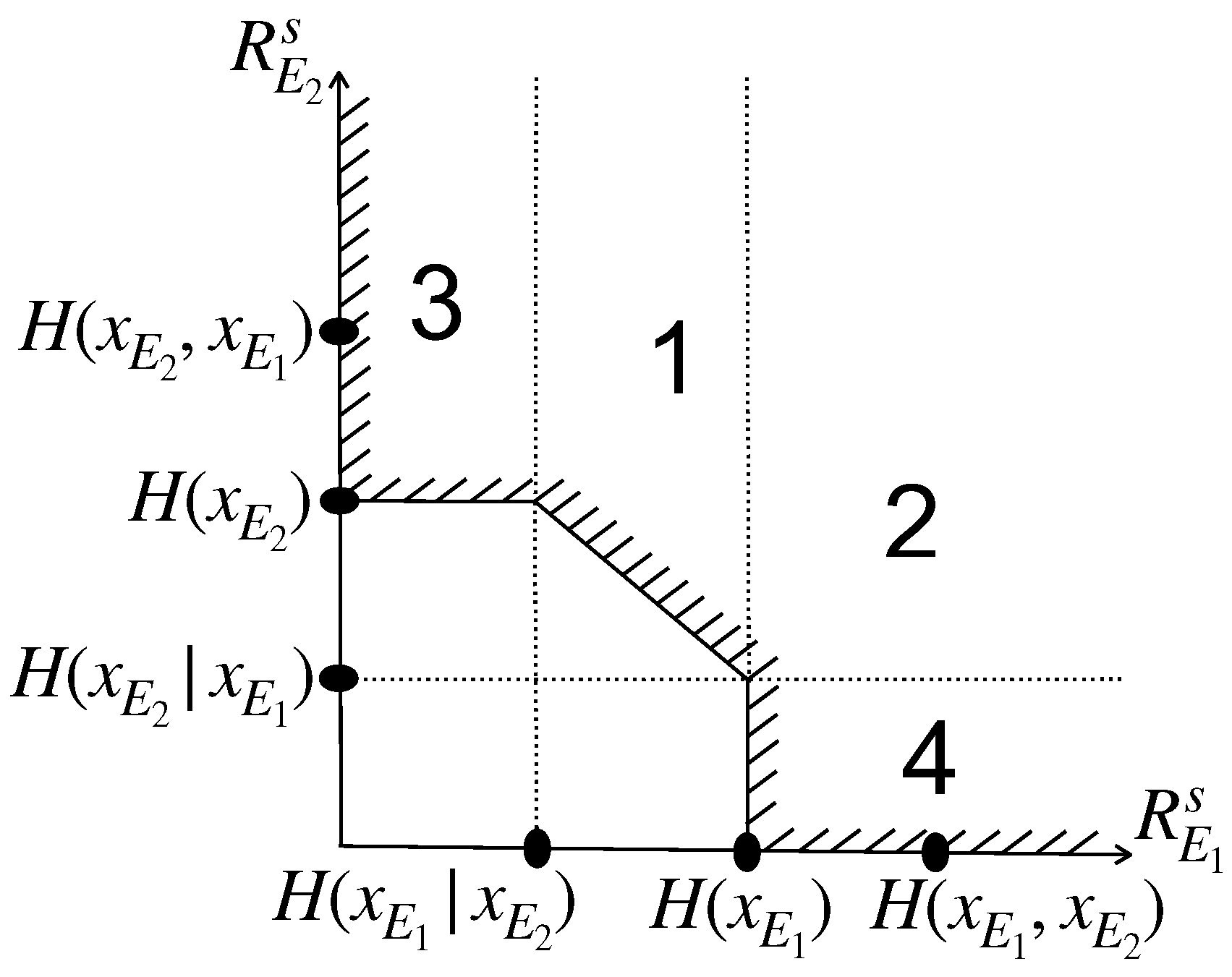
is computed with integrals of the probability density function (PDF) of the instantaneous SNRs within the rate region of inadmissibility. 4.6. Analyses for Inadmissible Rate Region for Chief Executive Officer (CEO) Problem with Slepian-Wolf Coding Let U represent the messages transmitted by Alice, and
and Since
and According to the Slepian-Wolf theorem, since
and In this context,
and In the case when both
and 4.7. Formulation of CEO Problem For a binary source,
, For a Gaussian source
, we have Let
and to assess the probability of error propagation using
represents a positive number that is arbitrarily smaller, and 4.8. Outage Probability at Bob
in Equation (24) is represented as
represents a function for sequential decoding associated with the decoding scheme. For a detailed explanation of the function 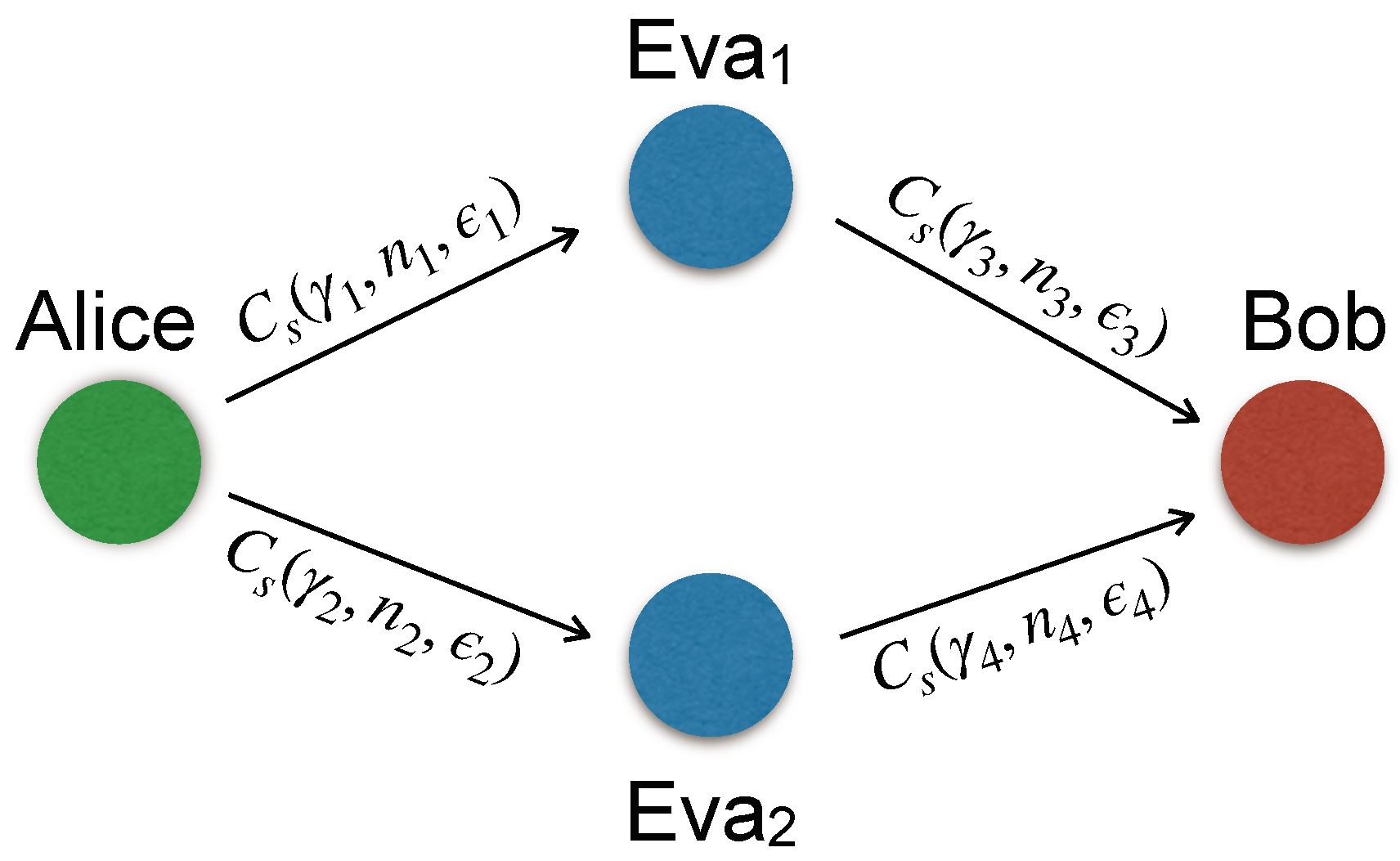
5.1. Reliable-and-Secure Probability Calculation Since Alice-Eva transmission error is allowed, the
-Bob ( Please note that, the outage happens when the distortion
outstrips When connect the rates
and and The derivation of the explicit expressions for Equations (36)–(39) may prove to be extremely challenging, due to the computational complexity of
. However, we introduce Monte Carlo simulations to compute
is also influenced by the levels of Figure 7 illustrates the relationship between the RSP and the average SNR, with varying values of error probability
as a key parameter. Additionally, reliable-and-secure probabilities are shown for the infinite block length scenario as a comparative reference. The infinite block length performance curves are also influenced by As observed in Figure 7, the RSP with short packets initially increases and subsequently declines as the average SNR increases. This trend reveals that enhancing the SNR does not always lead to a higher RSP. With increasing SNR, both the first and second terms
in Equation (18) increase simultaneously. Furthermore, an increase in the SNR of the Alice-Eva(s) links leads to higher probabilities of correct decoding at the relays, ultimately decreasing the total RSP. However, the RSP attains the peak value when the Alice-Eva and Eva-Bob link contributions are balanced. 5.2. Relays Location with RSP We focus on the relationship between the untrusted relay locations and the RSP. We reformulate the RSP equation as functions of the relay positions by incorporating the geometric gain. With
represents the path loss exponent Suppose, the distance between Alice and Bob is By substituting Equation (41) into Equations (36)–(39), we obtain the RSP expressions as functions of the untrusted relay positions. Comprehensive optimization has been formulated with respect to
as: 5.3. Optimization Strategy with Cooperative Jamming Here, we demonstrate an approach to improve the RSP with allocating transmission power between Alice,
optimally, The main challenge is determining the optimal values for
and Then, we formulate the optimization issue to: Notionally, by computing the partial derivatives to
and 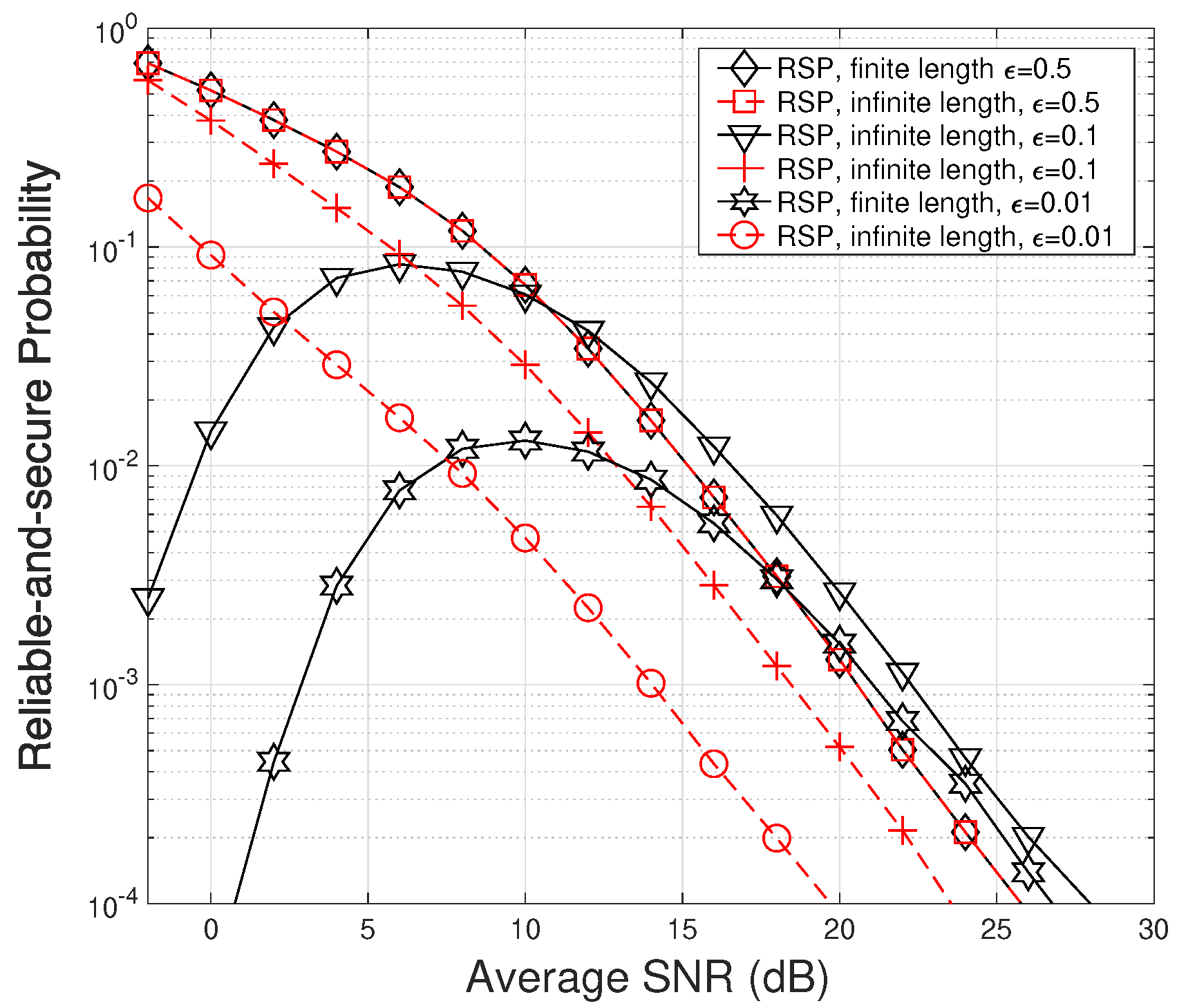
6.1. Implementation Considerations and Challenges The optimization of RSP involves solving non-linear equations with multiple constraints, which may require significant computational resources. Real-time deployment demands efficient algorithms capable of rapid convergence. Variations in channel conditions, such as fading and mobility, require the optimization process to adapt dynamically. Traditional methods may not respond effectively to such rapid changes, necessitating adaptive approaches. Deploying these strategies on resource-constrained devices (e.g., IoT sensors) may pose challenges due to limited processing power and energy availability. Lightweight approximations or machine learning models could mitigate these issues. To validate the proposed RSP metric under practical conditions, future work will leverage software-defined radios (SDRs) to simulate real-world environments. SDRs will allow testing of dynamic network scenarios, including varying relay positions, finite blocklength constraints, and power allocation strategies, while accounting for hardware-induced noise and interference. A testbed using platforms like GNU Radio and USRP will emulate the roles of source, untrusted relay, and destination to measure RSP and optimize performance. Insights from these experiments will guide the design of full-scale field tests, ensuring the robustness and practicality of RSP-based strategies for 5G/6G applications. 6.2. Open Issues in Secure Relay Networks There are several unsolved challenges in secure relay networks, particularly when it comes to achieving efficient and secure communication in the presence of untrusted relays. One major issue is the development of efficient relay selection algorithms. Current methods often do not account for the complexity of the environment, such as varying channel conditions and the dynamic behavior of untrusted nodes. Additionally, the optimal relay selection under power and security constraints remains computationally intensive, especially when the network grows in scale. Another critical open issue is the implementation of PLS in complex environments, such as those characterized by block fading, short-packet communications, or high mobility (e.g., vehicular networks). These scenarios introduce new challenges for maintaining high secrecy performance due to rapid channel variations and limited transmission opportunities. Addressing these issues requires more adaptive and efficient approaches that can dynamically optimize security and reliability in real-time. 6.3. Future Directions in PLS The future of PLS lies in expanding its applicability and robustness in more demanding and dynamic environments. One key direction is the development of adaptive power allocation strategies for secure communication. As outlined in the optimization problems discussed earlier, balancing transmit power between trusted and untrusted nodes while maximizing RSP is non-trivial. Future research should focus on efficient numerical methods or approximate closed-form solutions for real-time optimization, especially in the presence of finite block-length constraints. Machine learning (ML) and AI-based approaches are likely to play a significant role in advancing PLS. These techniques could be leveraged to predict channel conditions and optimize secure communication strategies dynamically. The integration of reinforcement learning to adaptively select relay nodes and power allocations based on real-time network conditions is another direction worth exploring. Reinforcement learning algorithms could dynamically optimize power allocation and relay selection by continuously learning from real-time network conditions. These methods can significantly reduce computational overhead while adapting to channel variations, making them suitable for high-mobility scenarios [31,32]. Non-orthogonal multiple access (NOMA) is another key area for future research, particularly in improving spectral efficiency and security for short-packet communications. The integration of PLS with NOMA schemes could further enhance secure communications in highly dense IoT environments, which are expected to proliferate with the advent of 6G. Combining PLS with NOMA could improve spectral efficiency and security in densely connected environments like IoT networks. As the adoption of emerging technologies like 5G/6G and edge computing accelerates, physical layer security must evolve to keep pace with the increasing complexity and demands of these systems. One key research direction is integrating PLS with edge computing to offload security-sensitive computations and leverage distributed resources for enhanced secrecy. This could involve designing secure offloading mechanisms that ensure confidentiality even when processing data near untrusted nodes or networks.
This paper investigates the performance and security challenges associated with PLS in lossy untrusted relay networks, particularly under the constraints of finite blocklength. The main contributions is the development of a RSP metric, which quantifies the likelihood of successful message recovery at the destination while ensuring the confidentiality of the message from untrusted relays. A key challenge addressed is the impact of decoding errors at the relays, which are allowed under the lossy DF setup. The paper further explores optimal power allocation and relay location strategies to enhance RSP performance. The numerical analyses demonstrates that even in the presence of imperfect decoding and lossy channels, optimal resource allocation can significantly improve the reliability and security. Practical implications of these findings are highly relevant for the design of secure communication systems in emerging 5G/6G networks, particularly in the contexts of uRLLC and mMTC.
| AF | Amplify-and-Forward |
| AWGN | Additive White Gaussian Noise |
| BER | Bit Error Rate |
| CEO | Chief Executive Officer |
| DF | Decode-and-Forward |
| i.i.d. | Independent and Identically Distributed |
| IoT | Internet of Things |
| MIMO | Multi-Input Multi-Output |
| ML | Machine Learning |
| mMTC | Massive Machine-Type Communications |
| NOMA | Non-Orthogonal Multiple Access |
| PLS | Physical Layer Security |
| RSP | Reliable-and-Secure Probability |
| SDR | Software-Defined Radio |
| SNR | Signal-to-Noise Ratio |
| TDMA | Time Division Multiple Access |
| uRLLC | Ultra-Reliable Low-Latency Communications |
S.Q.: Conceptualized and designed the research study, developed the methodology, wrote the software, and conducted formal analysis and investigations. Managed the data curation and performed the visualization of the results. Authored the original draft and actively participated in reviewing and editing the manuscript. M.C.: Supervised the research project and was responsible for project administration and securing funding. Provided significant intellectual contributions and participated in reviewing and editing the manuscript. Collaborated in conceptualizing the research study and played a critical role in validating the results.
Data supporting the results of this study are available upon request from the corresponding author.
Not applicable.
The authors declare no conflicts of interest regarding this manuscript.
No external funding was received for this research.
Declared None.
[1] Poor, H.V.; Schaefer, R.F. Wireless Physical Layer Security. Proc. Natl. Acad. Sci. USA 2017, 114, 19–26. [CrossRef] [PubMed]
[2] Xie, N.; Li, Z.; Tan, H. A Survey of Physical-Layer Authentication in Wireless Communications. IEEE Commun. Surv. Tutor. 2021, 23, 282–310. [CrossRef]
[3] Wang, W.; Teh, K.C.; Li, K.H. Relay Selection for Secure Successive AF Relaying Networks with Untrusted Nodes. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2466–2476. [CrossRef]
[4] Hu, H.; Gao, Z.; Liao, X.; Leung, V.C.M. Secure Communications in CIoT Networks with a Wireless Energy Harvesting Untrusted Relay. Sensors 2017, 17. [CrossRef] [PubMed]
[5] Sun, L.; Ren, P.; Du, Q.; Wang, Y.; Gao, Z. Security-Aware Relaying Scheme for Cooperative Networks with Untrusted Relay Nodes. IEEE Commun. Lett. 2015, 19, 463–466. [CrossRef]
[6] Zamir, N.; Ali, B.; Butt, M.F.U.; Javed, M.A.; Lee, B.M.; Ng, S.X. Cooperative Jamming-Assisted Untrusted Relaying Based on Game Theory for Next-Generation Communication Systems. Appl. Sci. 2023, 13. [CrossRef]
[7] Feng, C.; Wang, H.-M. Secure Short-Packet Communications at the Physical Layer for 5G and Beyond. IEEE Commun. Stand. Mag. 2021, 5, 96–102. [CrossRef]
[8] Feng, C.; Wang, H.-M.; Poor, H.V. Reliable and Secure Short-Packet Communications. IEEE Trans. Wirel. Commun. 2022, 21, 1913–1926. [CrossRef]
[9] Durisi, G.; Koch, T.; Popovski, P. Toward Massive, Ultrareliable, and Low-Latency Wireless Communication with Short Packets. Proc. IEEE 2016, 104, 1711–1726. [CrossRef]
[10] Yang, W.; Schaefer, R.F.; Poor, H.V. Wiretap Channels: Nonasymptotic Fundamental Limits. IEEE Trans. Inf. Theory 2019, 65, 4069–4093. [CrossRef]
[11] Tang, L.; Chen, H.; Li, Q. Social Tie Based Cooperative Jamming for Physical Layer Security. IEEE Commun. Lett. 2015, 19, 1790–1793. [CrossRef]
[12] Vo, V.N.; Tran, D.-D.; So-In, C.; Tran, H. Secrecy Performance Analysis for Fixed-Gain Energy Harvesting in an Internet of Things with Untrusted Relays. IEEE Access 2018, 6, 48247–48258. [CrossRef]
[13] Xiong, J.; Cheng, L.; Ma, D.; Wei, J. Destination-Aided Cooperative Jamming for Dual-Hop Amplify-and-Forward MIMO Untrusted Relay Systems. IEEE Trans. Veh. Technol. 2016, 65, 7274–7284. [CrossRef]
[14] Salem, A.; Musavian, L. NOMA in Cooperative Communication Systems with Energy-Harvesting Nodes and Wireless Secure Transmission. IEEE Trans. Wirel. Commun. 2021, 20, 1023–1037. [CrossRef]
[15] Zhao, S.; Liu, J.; Shen, Y.; Jiang, X.; Shiratori, N. Secure and Energy-Efficient Precoding for MIMO Two-Way Untrusted Relay Systems. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3371–3386. [CrossRef]
[16] Kuhestani, A.; Mohammadi, A.; Yeoh, P.L. Optimal Power Allocation and Secrecy Sum Rate in Two-Way Untrusted Relaying Networks with an External Jammer. IEEE Trans. Commun. 2018, 66, 2671–2684. [CrossRef]
[17] Lv, L.; Zhou, F.; Chen, J.; Al-Dhahir, N. Secure Cooperative Communications with an Untrusted Relay: A NOMA-Inspired Jamming and Relaying Approach. IEEE Trans. Inf. Forensics Secur. 2019, 14, 3191–3205. [CrossRef]
[18] Qian, S. Reliable and Secure Short-Packet Communications in Untrusted Diamond Relay Networks. IEEE Access 2023, 11, 24686–24695. [CrossRef]
[19] Qian, S. Optimal power allocation for secure transmission in untrusted relay networks with Alamouti space-time block coding. IEICE Commun. Express 2024, 13, 496–499. [CrossRef]
[20] Qian, S.; Cheng, M. An Optimization Strategy for Security and Reliability in a Diamond Untrusted Relay Network with Cooperative Jamming. Network 2024, 4, 405–425. [CrossRef]
[21] Gamal, A.E.; Kim, Y.-H. . Network Information Theory ; Cambridge University Press: Cambridge, UK, 2011; . .
[22] Qian, S.; Zhou, X.; He, X.; He, J.; Juntti, M.; Matsumoto, T. Performance Analysis for Lossy-Forward Relaying Over Nakagami-m Fading Channels. IEEE Trans. Veh. Technol. 2017, 66, 10035–10043. [CrossRef]
[23] Wan, D.; Wen, M.; Ji, F.; Yu, H.; Chen, F. On the Achievable Sum-Rate of NOMA-Based Diamond Relay Networks. IEEE Trans. Veh. Technol. 2019, 68, 1472–1486. [CrossRef]
[24] Kara, F.; Kaya, H. Error Probability Analysis of NOMA-Based Diamond Relaying Network. IEEE Trans. Veh. Technol. 2020, 69, 2280–2285. [CrossRef]
[25] Xiang, Z.; Yang, W.; Cai, Y.; Ding, Z.; Song, Y.; Zou, Y. NOMA-Assisted Secure Short-Packet Communications in IoT. IEEE Wirel. Commun. 2020, 27, 8–15. [CrossRef]
[26] Polyanskiy, Y.; Poor, H.V.; Verdu, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [CrossRef]
[27] Gradshteyn, I.S.; Ryzhik, I.M. . Table of Integrals, Series, and Products ; Academic Press: New York, NY, USA, 2014; . . [CrossRef]
[28] Dong, L.; Han, Z.; Petropulu, A.P.; Poor, H.V. Improving Wireless Physical Layer Security via Cooperating Relays. IEEE Trans. Signal Process. 2010, 58, 1875–1888. [CrossRef]
[29] Zhou, X.; Yi, N.; He, X.; Hou, J.; Matsumoto, T.; Szott, S.; Gonzales, D.; Wolf, A.; Matthe, M.; Kuhlmorgen, S.; Adigun, O. ICT-619555 RESCUE Deliverable D1.2.1—Assessment on Feasibility, Achievability, and Limits. 2015 Available online: https://cordis.europa.eu/docs/projects/cnect/5/619555/080/deliverables/001-D55final.pdf (accessed on 13 November 2024).
[30] He, X.; Zhou, X.; Komulainen, P.; Juntti, M.; Matsumoto, T. A Lower Bound Analysis of Hamming Distortion for a Binary CEO Problem with Joint Source-Channel Coding. IEEE Trans. Commun. 2016, 64, 343–353. [CrossRef]
[31] Ara, I.; Kelley, B. Physical Layer Security for 6G: Toward Achieving Intelligent Native Security at Layer-1. IEEE Access 2024, 12, 82800–82824. [CrossRef]
[32] Hoang, T.M.; Vahid, A.; Tuan, H.D.; Hanzo, L. Physical Layer Authentication and Security Design in the Machine Learning Era. IEEE Commun. Surv. Tutor. 2024, 26, 1830–1860. [CrossRef]
We use cookies to improve your experience on our site. By continuing to use our site, you accept our use of cookies. Learn more